UX Essentials: Fitt’s Law
Many people perceive user interface design to be more of an art, opposed to a science. However, Fitt’s law is a mathematical equation which helps quantify the usability of user interfaces. Not just computer interfaces, but physical interfaces such as door handles, washing machine dials and cockpit interiors...
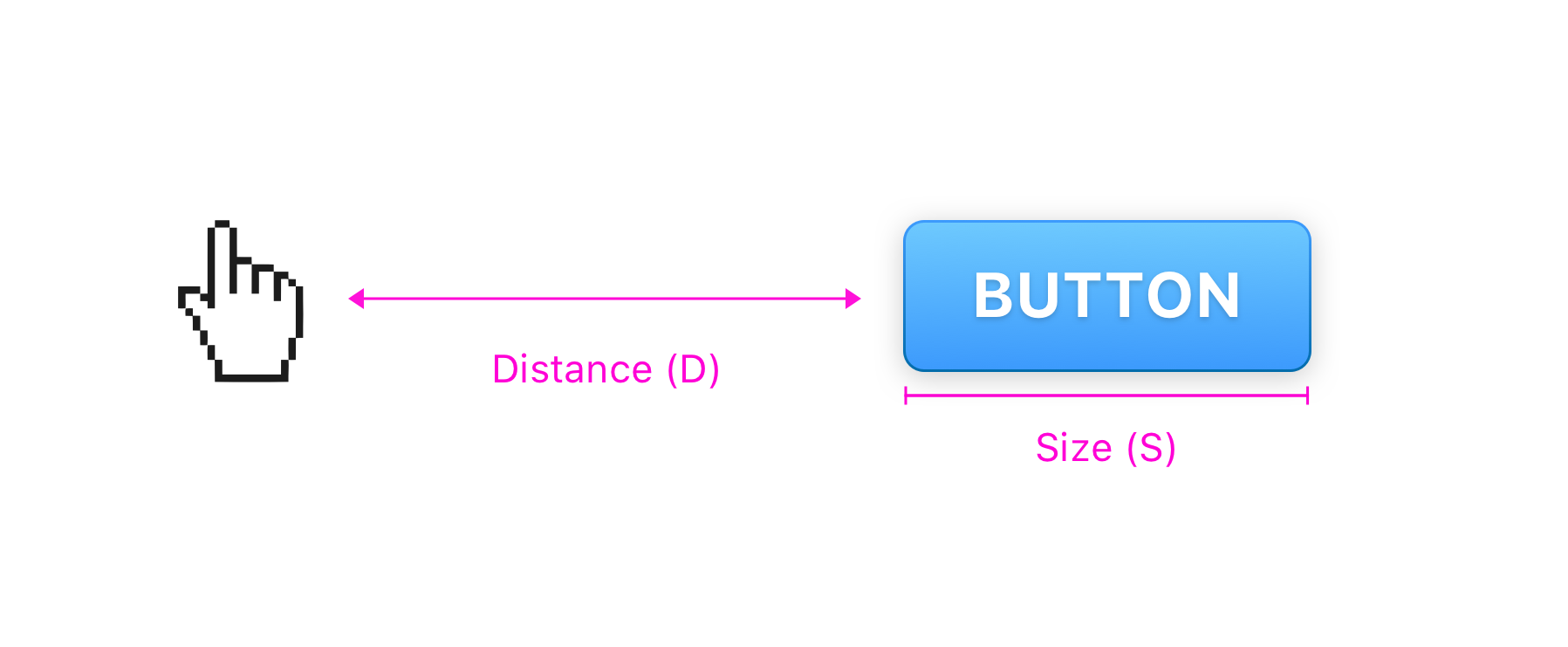
What this law tries to predict, is the time it takes for the user to move their cursor through distance (D) to the target of size (S). You want the distance to be as small as possible in every interface that you design; if a task takes less time to complete, the interface is considered more usable.
After all, improving efficiency and usability of a product is the backbone of successful user experience design
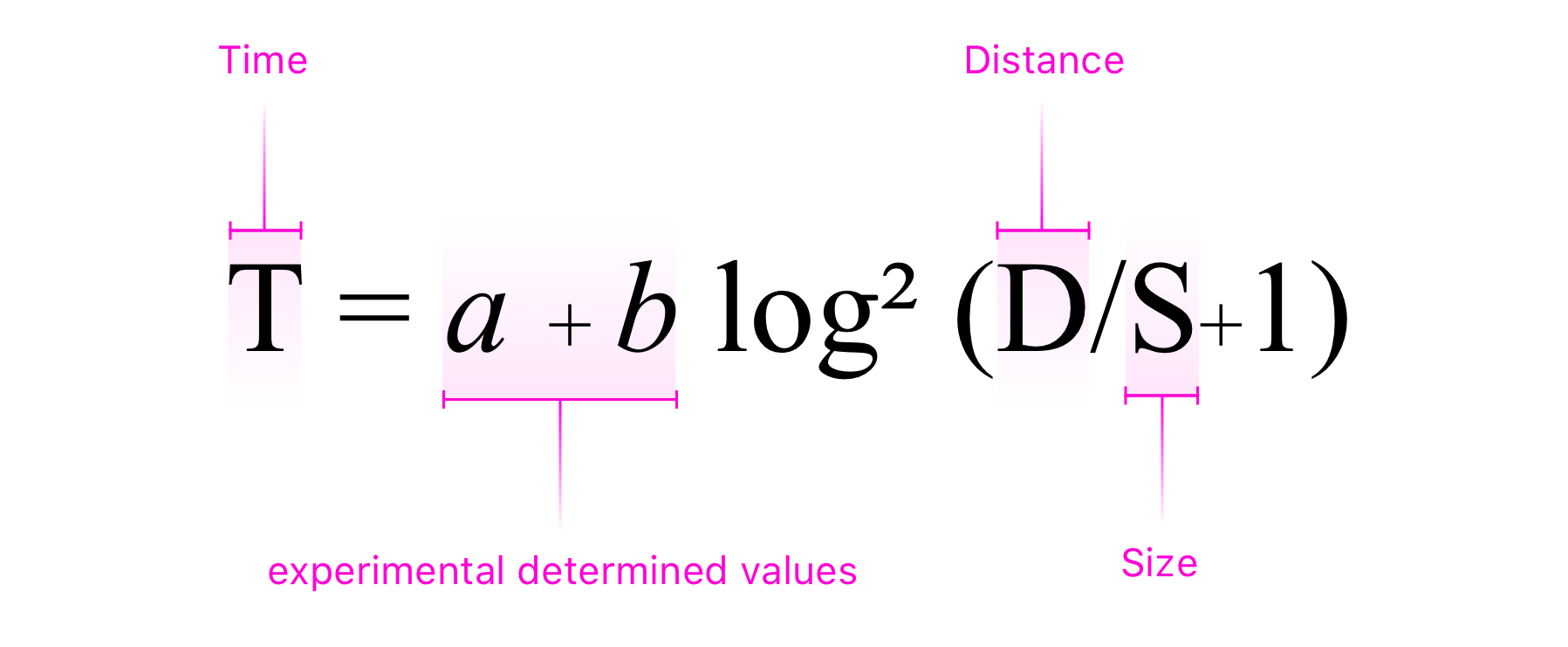
The mathematical formula, which was originally published in 1954 by Paul Maurice Fitts, looks something like this (figure 2). Albeit, the simplicity of this formula can be better understood visually in Figure 1.
It’s important to recognise you don’t need to be a mathematician to understand the basis of the law; the same way you don’t need to understand the chemical properties of ink to be able to write. The basis of the law can be somewhat simple to understand and consider within the design process on a practical level.
The academic texts are only applicable in scientific studies, or when designers wish to use it literally (usually those who are HCI “designers”).
However, for the benefit of being agile, and moving iteratively; it’s perhaps not wise to be loosing your sanity doing maths. The constant consideration alone is more beneficial than the minute percentage increase in conversion when implemented literally.
Mac vs Windows
The Mac vs Windows way of handling menu systems for applications is an easy way to identify how the consideration of Fitt’s law can better an entire operating system.
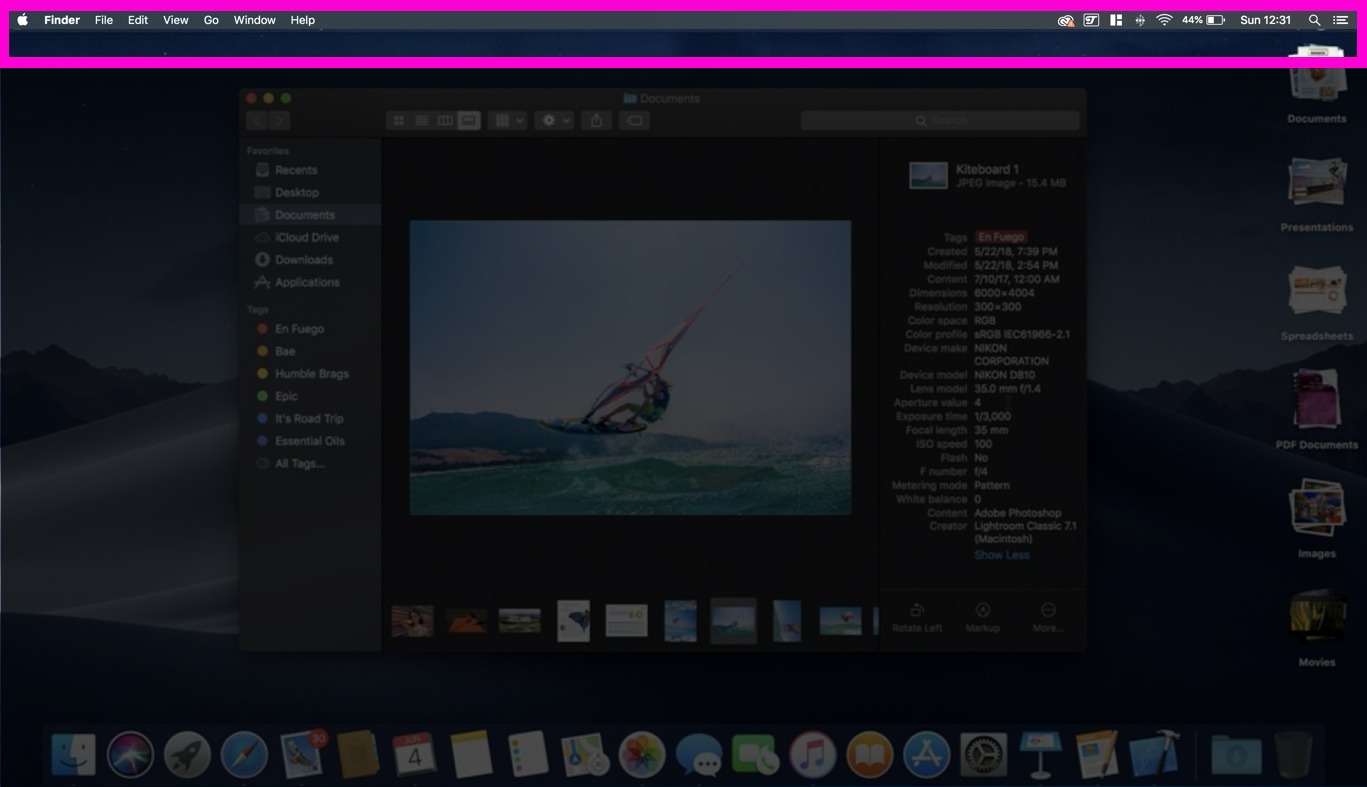
You can see on the Mac OS that you have the menu options at the top of the screen. This implementation of a menu bar doesn’t change, only the names of the menu options may change, based upon the selected application.
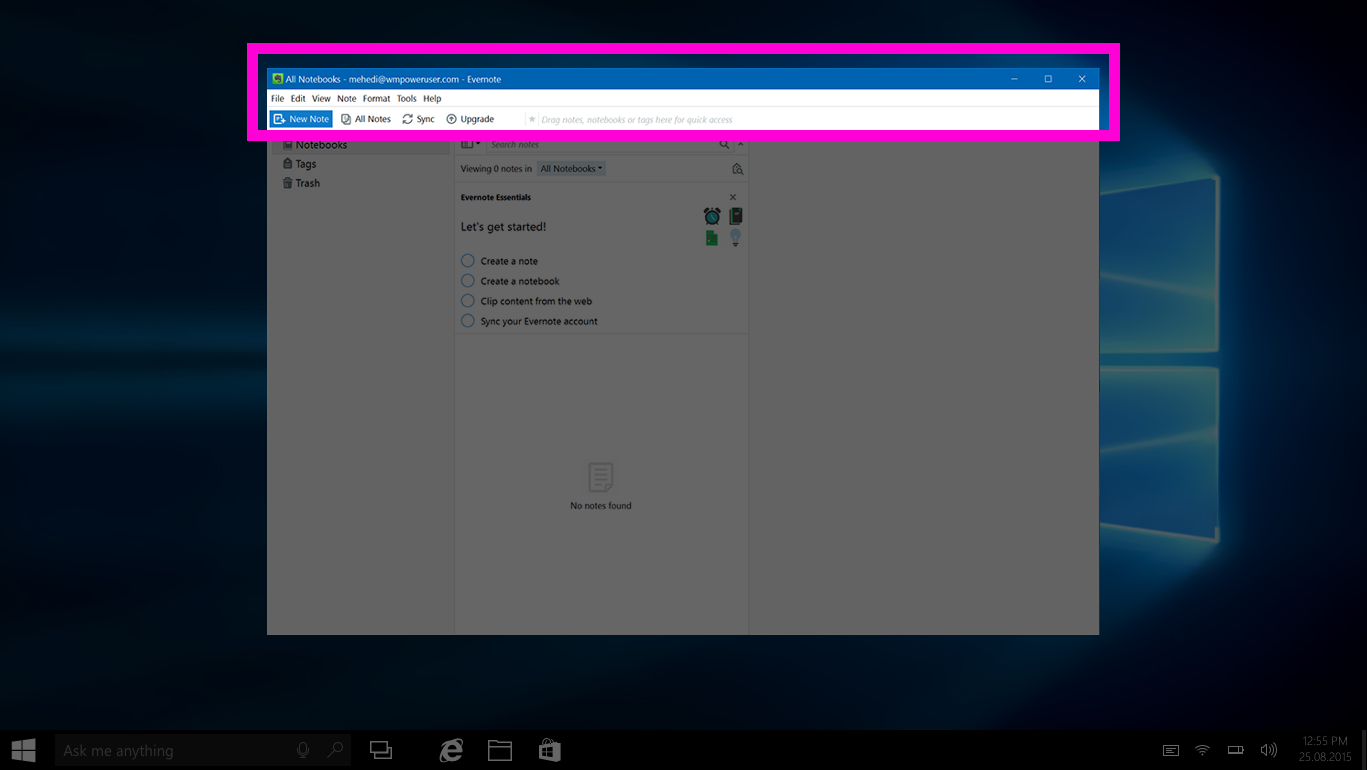
Opposed to the Windows OS, which chooses to have the menu options inside the application window. This implementation is not favourable when you calculate Fitt’s law.
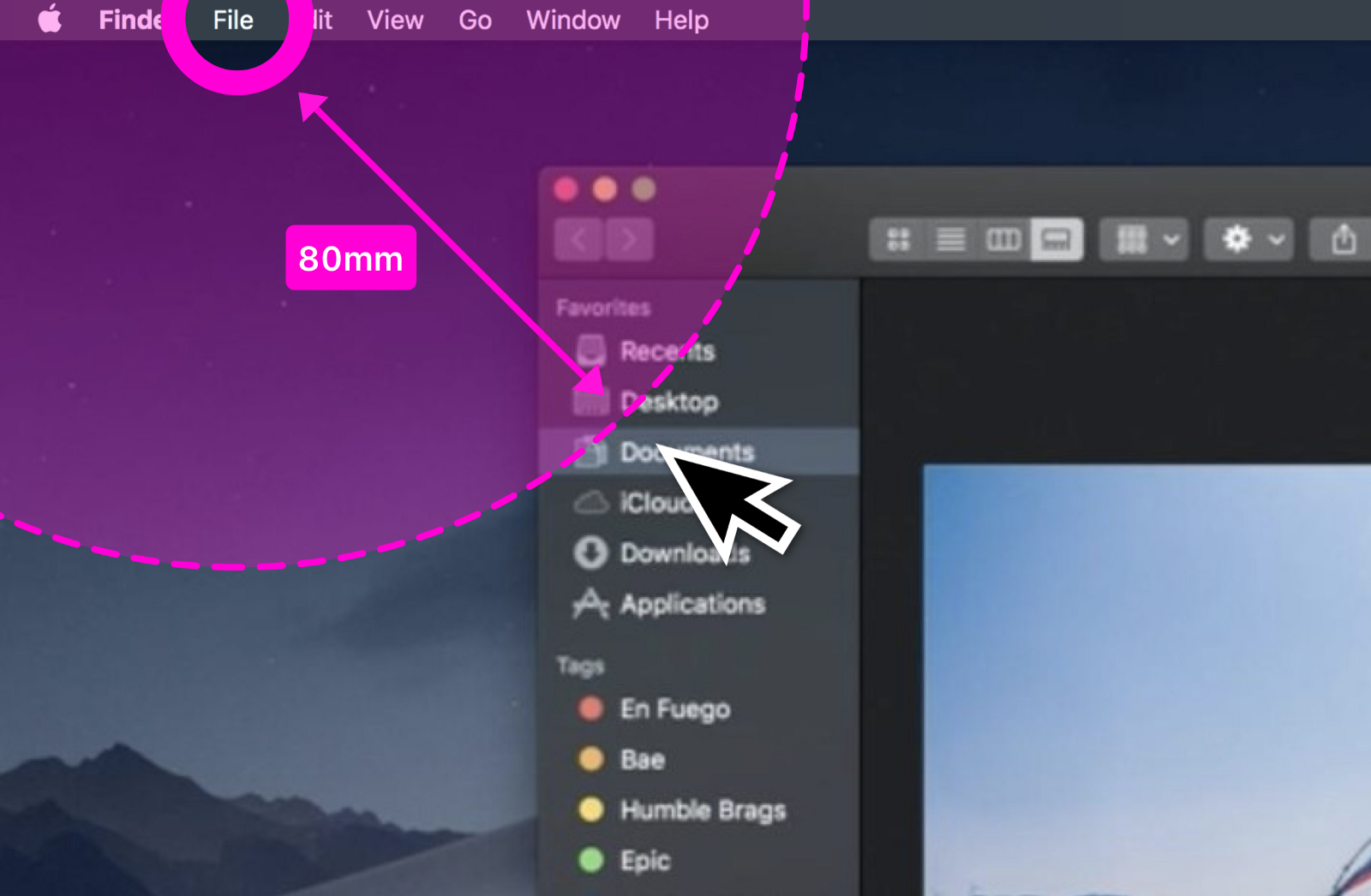
We can pick any measurement units to calculate the size and the difference, but If, for arguments sake, we calculate the time it takes for a user to move the cursor 80mm (D) to the target (S) on the Mac OS menu system, we can compare those results with the Windows implementation and see which one takes the smallest amount of time for a user to navigate.
The Mac OS has the menu options at the top of the screen (Figure 3 and 5), this means we can assume the target area and size is arbitrarily bigger than the Windows OS (Figure 4 and 7), as it reduces the chances of the user overrunning the cursor past the target. The physical screen actually makes the target area in figure 5 significantly larger. So lets make the target 50mm in this instance.
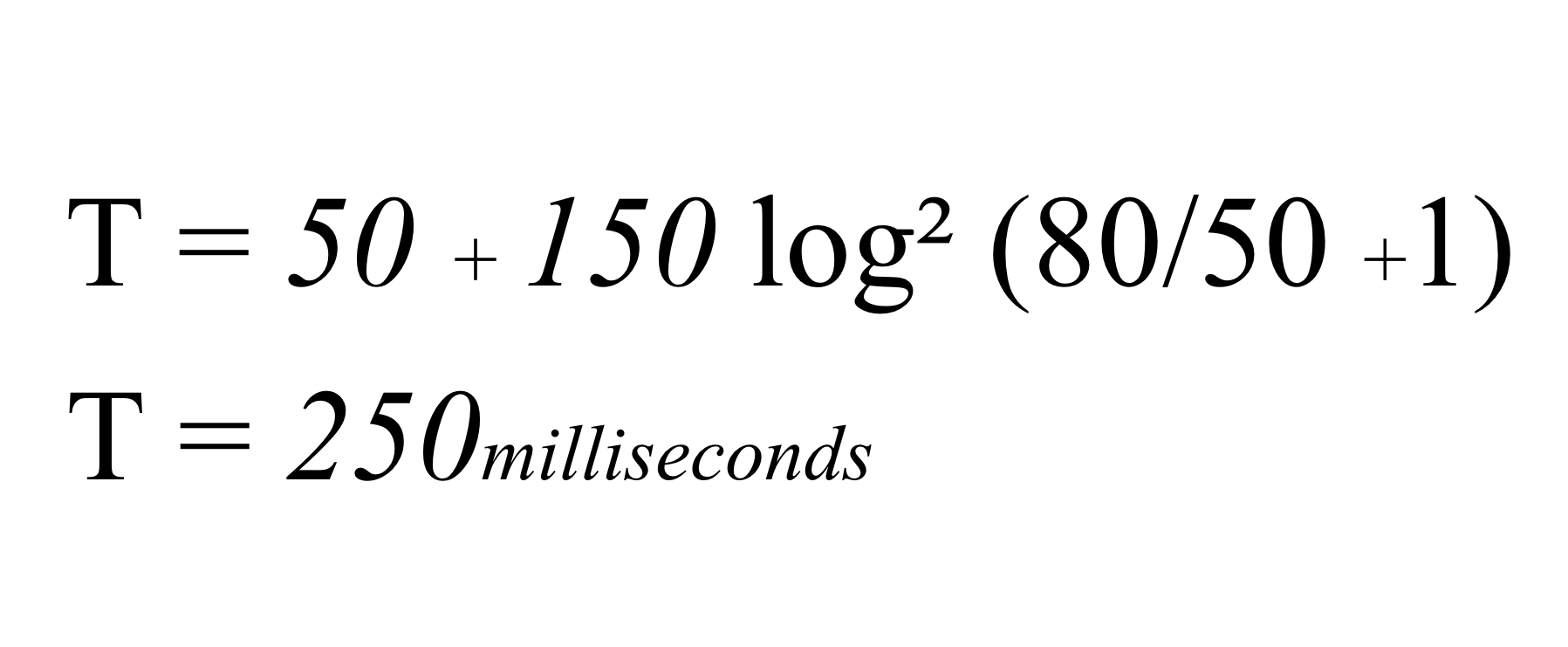
This would make the formula look something like this, and the time it takes for the user to move the cursor 80mm to the 50mm target would be 250milliseconds. (If you’re wondering where I got the 50 + 150 from; these are irrelevant as they’re simply experimentally determined values).
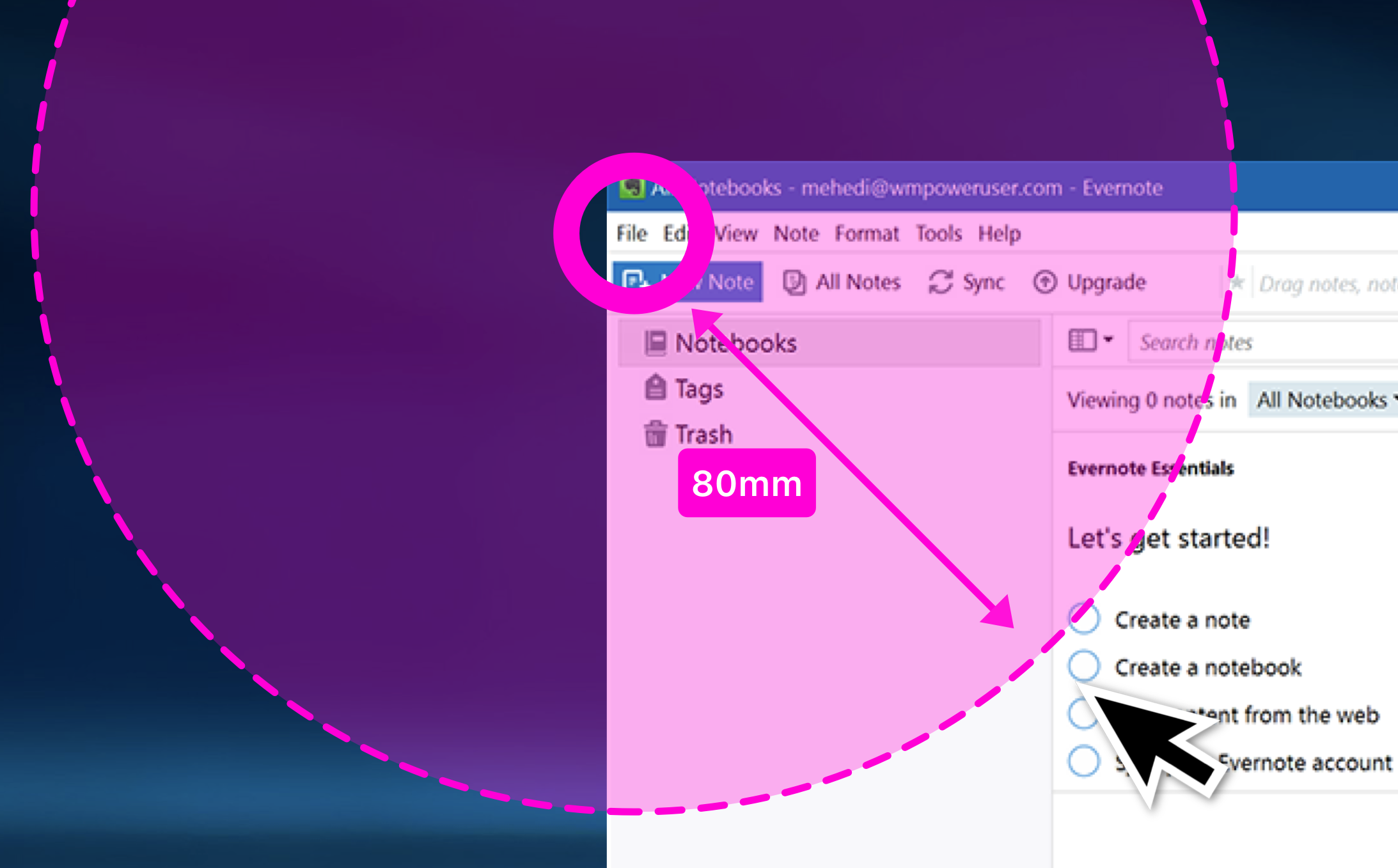
The Windows implementation (figure 7) significantly increases the chances of overrunning the target area, which statistically makes the target smaller as there are no boundaries to stop the user overrunning the action. This makes the size of the target defined and therefore makes the size of the target much easier to calculate and would probably be around 5mm.
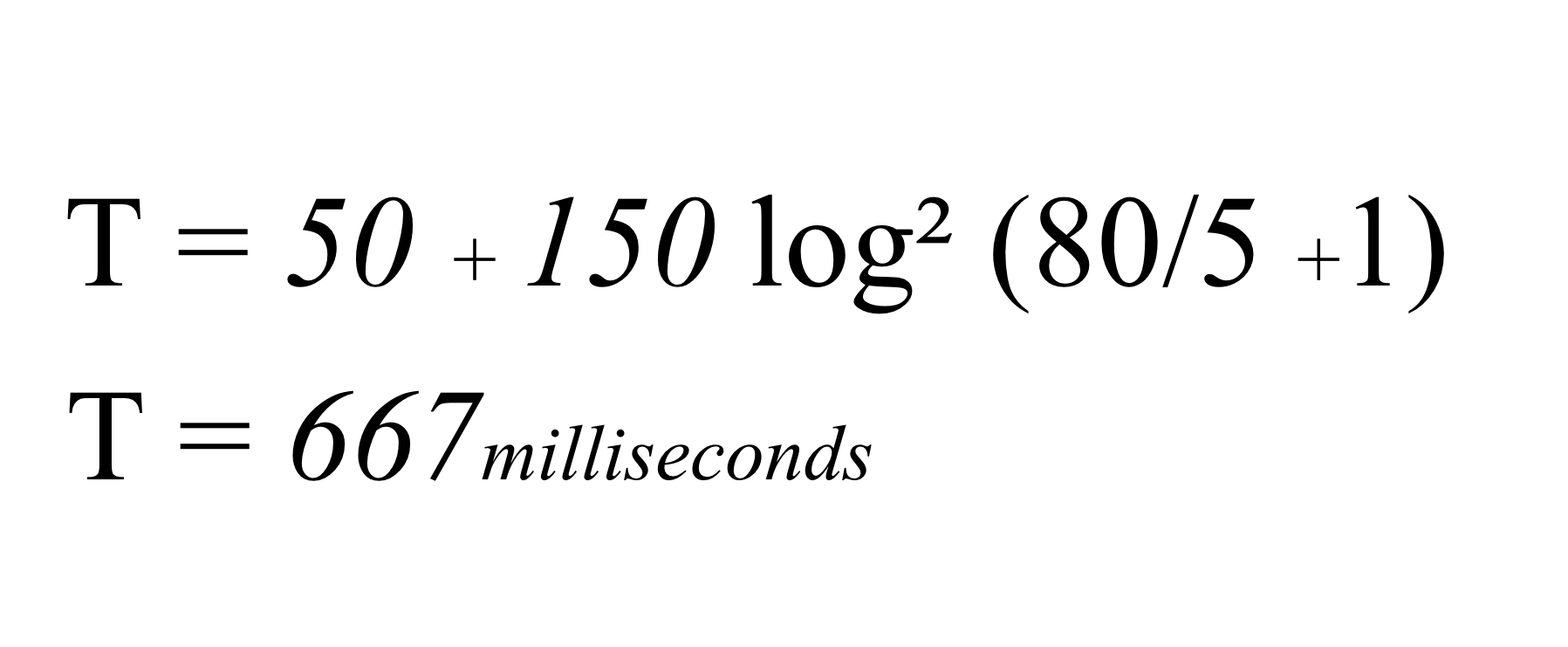
When you calculate these differences, the time increases by 3 times to 667milliseconds on the Windows OS. Proving the menu system on Windows is 3 times slower to navigate on average, than the Mac OS in this instance*
This could be a contributing factor as to why many people find the Mac OS a lot easier to use, and why their software is considered to be more dominant not only in terms of aesthetics albeit practicality, too.
Of course, they’ll be many loyal Windows users with cognitive bias to scream from the rooftops so say they find the Mac OS “horrible to use”. But these are the benefits of quantitative mathematical formulas. They help identify and study how people perceive user interfaces. Years of practice and routine would certainly be a factor if you tried to study a loyal Windows OS user transferring over to Mac OS.
*These calculations are by no means accurate. They’re simply fabricated to demonstrate how to use Fitt’s Law works and how it can be applied to a real life situation
Thank you for checking out this blog. You can see more of my work on my website, darceybeau.co.uk, or my Dribbble profile, or my Behance profile. You can email me about working together at info@darceybeau.co.uk. You can also follow me on Twitter, Instagram, or Unsplash. Have a great day!

